Расчет максимальной глубины разрушения (МГР)
Расчет прогнозной максимальной глубины разрушения проводится по результатам толщинометрии трубопровода или образцов.
В некоторых публикациях распределение коррозионных повреждений описывают нормальным или логарифмически-нормальным законом. Однако, чаще исследователи описывают распределение глубин проникновения коррозии законом экстремальных значений (двойным экспоненциальным или распределением Гумбеля). Данные, подтверждающие это, приведены в работах: Маннапов Р.Г. Оценка надежности оборудова-ния по распределению дефектов. -Химическое и нефтяное машиностроение, 1989, № 1,с 27-29. , Коллинз Дж. Повреждение материалов в конструкциях: Анализ, предсказание, предотвращение. Пер. с анг. - М.: Мир, 1984., Provan J.W., Rodriguez E.S. Development of a Markov description of pitting corrosion. - Corrosion (USA), 1989, - 45, N 3, p 178 - 192.
Методика была разработана А.И. Оводовым в ГУП «ИПТЭР», но не вошла ни в какие в руководящие документы ввиду закрытия финансирования по проекту, заказанному Миннефтепромом в 90-е годы.
Методика основана на обработке результатов коррозионных измерений с использо-ванием распределения Гумбеля (двойное экспоненциальное), которому как было заме-чено в работах различных исследователей подчиняются максимальные или минималь-ные значений многих выборок статистических данных, например, максимальное или минимальное месячное количество осадков. Одним, из хорошо описываемых этим рас-пределением явлений, является распределение глубин максимальных язв локальной коррозии.
Получив закон распределения по некоторому объему данных толщинометрии на не-большом участке, можно с определенной вероятностью спрогнозировать глубину язв на большем участке площади.
Методика Расчета МГР
Методика, заложенная в расчет в данном окне программы приведена ниже:
1.1 Из выборки глубин разрушений {xji}, полученной по результатам толщиномет-рии, на каждой единичной площадке отыскивается экстремальное (максимальное) зна-чение Xi и формируется выборка экстремальных (максимальных) значений глубин раз-рушения, число которых равно числу единичных площадок N.
1.2 Определяется среднее арифметическое выборки экстремальных значений глу-бин разрушения по формуле:
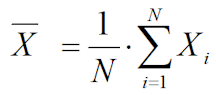
1.3 Определяется стандартное отклонение выборки экстремальных значений, по формуле:
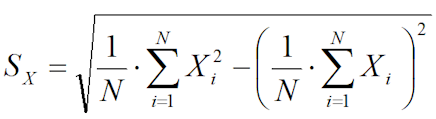
1.4 Определяется коэффициент вариации выборки экстремальных значений глубин разрушения, по формуле:
1.5 Определяются оценки параметров распределения экстремальных глубин разрушения:
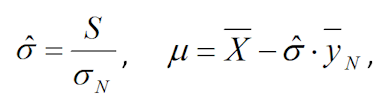
где
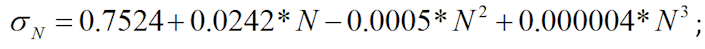
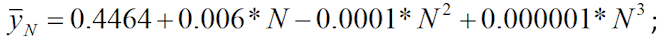
1.6 Проводится оценка однородности эмпирической выборки экстремальных значений глу-бин разрушения, для чего эмпирическая выборка экстремальных значений глубин раз-рушения упорядочивается по возрастанию в виде вариационного ряда х1< х2<…<xN и вы-числяются эмпирические значений накопленных частот:
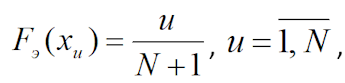
для каждого значения xu вычисляются теоретические значения накопленных частот:
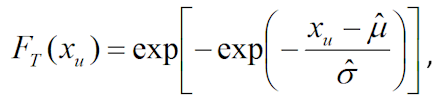
вычисляются абсолютные значения разностей:
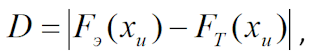
среди которых находится максимальное значение:
Величина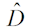 
сравнивается с критическими значениями критерия Колмогорова-Смирнова 
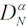определяемого по формуле:
Расчет критерия 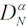проводится для уровня значимости α = 0,01. Выполнение усло-вия 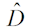< 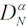означает подтверждение гипотезы о соответствии полученной выборки рассматриваемому закону распределения. Если наблюдается 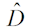>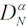, то это служит критерием выделения соответствующего значения xu и его отбраковки. После чего по-вторяется процедура проверки однородности эмпирической выборки экстремальных значений.
1.7 Вычисляется значение масштабного фактора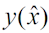 
, при котором наблюдается искомая точечная оценка МГР 
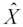с заданной доверительной вероятностью q* = 0,5:
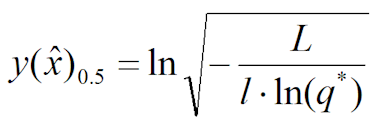
1.8 Определяется искомая точечная оценка 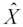максимальной глубины разрушения:
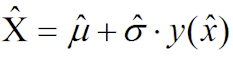
1.9 Для вычисления среднеквадратического отклонения оценки МГР определяется значение масштабного фактора для доверительной вероятности равной q* = 0,95:
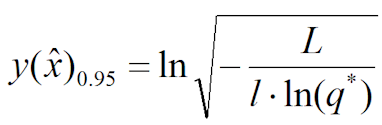
1.10 Рассчитывается значение среднеквадратического отклонения оценки МГР по формуле:
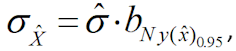
где
1.11 Определяется относительная ошибка оценки МГР:
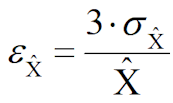
1.12 Рассчитывается наблюдаемая максимальная скорость коррозии трубопровода:
где Хmax – максимальное, наблюдаемое на момент толщинометрии, значение глуби-ны коррозионного повреждения трубопровода;
∆Т – период времени (лет) между вводом объекта в эксплуатацию и датой толщи-нометрии.
1.13 Рассчитывается оцениваемая максимальная скорость коррозии трубопровода:
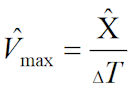
1.14 Рассчитывается максимальная остаточная толщина стенки трубопровода с учетом среднеквадратического отклонения оценки максимальной глубины разрушения:
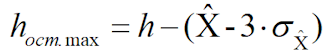
где h – исходная толщина стенки трубопровода.
1.15 Рассчитывается минимальная остаточная толщина стенки трубопровода с учетом среднеквадратического отклонения оценки максимальной глубины разрушения:
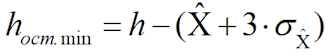
1.16 Определяется дата возникновения отказа с учетом ошибки оценки МГР:
1.16.1 Минимальное значение времени до возникновения отказа:
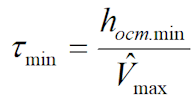
1.16.2 Максимальное значение времени до возникновения отказа:
1.16.3 Если максимальная остаточная толщина стенки трубопровода превышает исходное зна-чение толщины трубопровода, то в качестве даты отказа принимается дата толщиномет-рии и рассчитывается вероятность возникновения отказа на момент толщинометрии равная вероятности попадания оценки МГР в диапазон между исходной толщиной тру-бопровода и верхней доверительной границей оценки МГР:
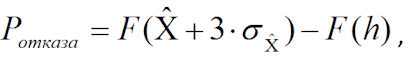
где 
– значение функции распределения экстремальных глубин разруше-ния, соответствующее верхней доверительной границе разброса оценки МГР (с довери-тельной вероятность равной 0,95) и определяемое по формуле:
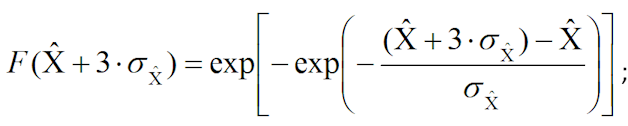
F(h) – значение функции распределения экстремальных глубин разрушения, соответ-ствующее исходной толщине трубопровода и определяемое по формуле:
